Ciao,
questa è Link Molto Belli, ecc. ecc. Come state? Spero tutto bene. Nel corso della pausa estiva si sono iscritte molte persone, ci tengo quindi a precisare che di solito qui ci sono link pazzi e interessanti.
Questa settimana però seguirò la tradizione per cui, a Ferragosto, mando un’edizione speciale della newsletter, tutta dedicata a un argomento. So che è passato qualche giorno da Ferragosto ma molti di voi sono ancora in vacanza, quindi oggi parliamo del cerchio.
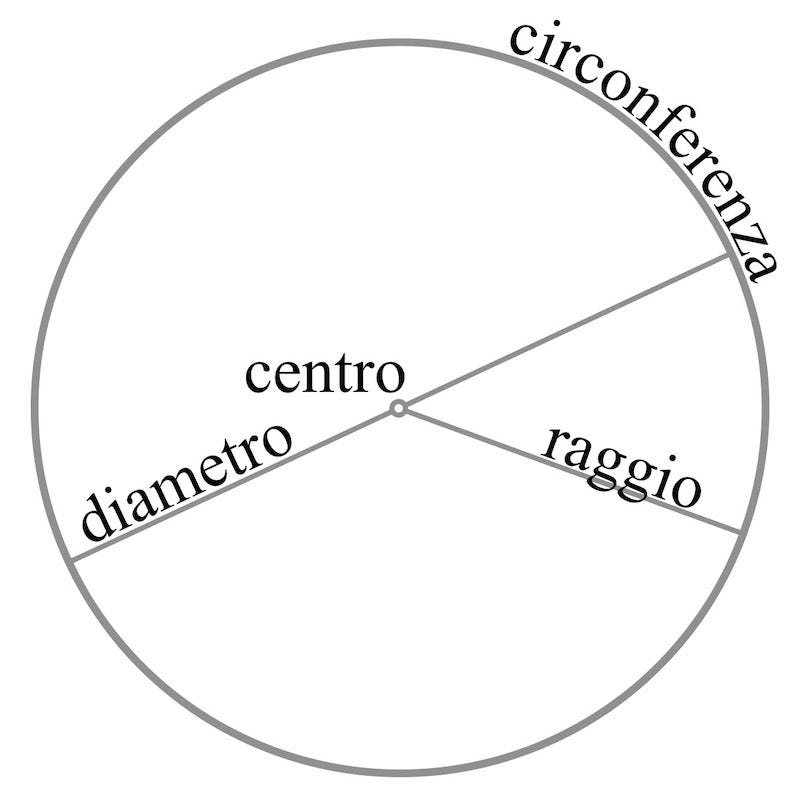
Immagine: Wikipedia
Questo qui sopra è un cerchio. Il suo perimetro si chiama circonferenza, al centro ha un centro (ehm), mentre il raggio è la metà del diametro. Oggi sappiamo tutti che la lunghezza di una circonferenza è pari al diametro (2r) moltiplicato per π. L’area totale del cerchio, invece, è il quadrato del raggio (r²) moltiplicato per π.
Ma che cos’è questo diavolo di π? È il famoso pi greco, una costante matematica che indica il rapporto tra la lunghezza di una circonferenza e il suo diametro, rapporto che rimane costante, qualunque sia il cerchio in questione. Se prendete un razzo, andate su Venere e, poco prima di morire nel modo peggiore possibile, disegnate un cerchio, il rapporto tra circonferenza e diametro sarà lo stesso risultato che dà dalla notte dei tempi in tutto l’Universo: tre e qualcosa.
A dispetto del suo nome, non furono i Greci a scoprire questa cosa. Si sapeva da molto tempo. Studiando la storia della matematica si scopre che tutti sapevano già tutto dalla notte dei tempi, solo che non avevano la calcolatrice. Come spesso succede, “la notte dei tempi” significa “al tempo dei Babilonesi”. Ecco, pare che i Babilonesi sapessero (quasi) tutto. Le stelle, la geometria, le equazioni: era già tutto lì. (Un’altra cosa che si scopre studiando la storia della matematica è che i Romani non erano per niente interessati ai numeri, a cui preferivano di gran lunga la guerra e le orge.)
Tornando a noi, i Babilonesi avevano calcolato questo misterioso rapporto tra le circonferenze e i loro diametri. Secondo i loro calcoli, era pari a 3,125. Per gli Egizi era invece uguale 4x(8/9)². Anche l’Antico Testamento parla di questo strano numero, che nella Bibbia è però arrotondato a 3. Senza virgole né niente, lol. Dai Libri dei Re leggiamo:
“Fece un bacino di metallo fuso di dieci cubiti da un orlo all'altro, rotondo; la sua altezza era di cinque cubiti e la sua circonferenza di trenta cubiti.”
Oggi sappiamo tutti quanto vale il pi greco. Inizia così con 3,1415926535 e va avanti all’infinito dopo la virgola. Usando potenti computeroni siamo arrivati a identificare miliardi e miliardi delle cifre di questo strano composto matematico. In questo sito trovate il primo milione.
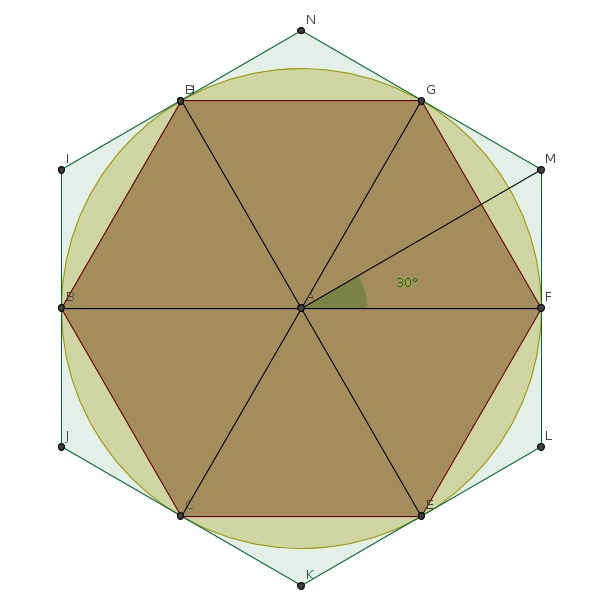
Tra le persone dell’antichità che si misero in testa di scovare il mistero di questo strano coso ci fu anche Archimede di Siracusa. Altri ci avevano provato prima e ci avrebbero provato dopo ma oggi parliamo di lui. Innanzitutto, Archimede decise di misurare la circonferenza di un cerchio con un metodo particolare, inscrivendovi un poligono. Per facilitarsi i calcoli, scelse un esagono regolare (il motivo è semplice: quando è inscritto in una circonferenza il suo perimetro è pari a sei volte il raggio del cerchio stesso).
L’esagono toccava la circonferenza in sei punti. Bastava immaginare un poligono con un numero infinito di lati per fare coincidere il suo perimetro con la circonferenza stessa. Sembra un ragionamento strano da fare in Sicilia due secoli prima di Cristo, ma tant'è, Archimede decise di provarci. Raddoppiò i lati del poligono. Ancora. E ancora. Lo fece fino ad arrivare a un poligono-mostro di 96 lati. Il nostro stava braccando il perimetro del cerchio, riempiendolo di lati, e quindi di vertici e quindi di punti. Al contempo, costruiva una figura simile al di fuori del cerchio, circoscritta alla circonferenza.
via Mateweb
Come raccontato da Petr Beckmann, autore di un ottimo libro sull’argomento , l’approccio di Archimede si basava sul fatto che «il perimetro di un poligono regolare di n lati inscritto in un cerchio è minore della sua circonferenza, mentre il perimetro di un poligono simile circoscritto a una circonferenza è maggiore della circonferenza». Oggi lo chiamiamo metodo di esaustione, perché di approssimazione in approssimazione va a completare una figura, esaurendola.
Archimede riuscì a localizzare la costante misteriosa, dimostrando che doveva avere un valore superiore a 3, senza però identificarla del tutto. Secondo i calcoli del nostro, infatti, π era compreso tra 3,14084 e il 3,142858.
A questo punto, la costante non era ancora un valore preciso, “più esotica di ogni altro numero”1. Archimede non sapeva bene cosa farsene, vivendo in un mondo in cui i numeri erano interi e positivi, al massimo frutto di frazioni (tipo 3/4). Questa costante era invece misteriosa, oscura, e lo sarebbe rimasta per qualche millennio.
Oggi sappiamo che π indica un numero irrazionale (decimale illimitato non periodico) e trascendente (poiché non è soluzione di alcuna equazione algebrica irriducibile a coefficienti interi). È un valore strano, magico, che compare e scompare nelle disquisizioni teoriche e negli studi più pratici, dà una rigida regolarità alla più tonda e sfuggevole delle forme geometriche, una figura perfetta e inafferrabile, così poco umana e così eterea, superiore al nostro piccolo mondo spigoloso e impuro. Sarà un caso ma è proprio la conquista del cerchio, l’impossibilità della sua quadratura e misura, a venire tirata in ballo da Dante Alighieri quando, nel Paradiso, viene illuminato dalla luce divina. Di fronte a Dio, il Poeta non sa proprio cosa dire, e allora che fa? Si mette a pensare ai cerchi:
Qual è 'l geomètra che tutto s'affige
per misurar lo cerchio, e non ritrova,
pensando, quel principio ond'elli indige, tal era io a quella vista nova.Come il geometra, che si impegna intensamente fare quadrare il cerchio, ma non riesce a trovare, pur pensandoci a fondo, il principio su cui basare il proprio calcolo,
così stavo io di fronte a quella straordinaria visione.
A sabato prossimo,
Pietro
Steven Strogatz, Il potere dell’infinito. L’universo raccontato dal calcolo infinitesimale, Codice Edizioni, 2021.



Figo! Ottima edizione!
magistrale